なんとなくわかる大学化学

大学化学をゆるゆると解説するブログです。

【なんとなくわかる量子化学】第４回　やっぱり解けないシュレディンガー方程式と

多体問題

　さて、前回までのお話で、π共役系のエネルギーを求めることができました。でも、もっと精度よく計算したいので、原子核も含めて分子のシュレディンガー方程式を解きたい所なのですが…
 

＿人人人人人人人人人人人人人人人人人人人人人人＿
＞　分子のシュレディンガー方程式は解けません　＜
￣Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^Y^￣


　これは数学的にわかっていることで、多体問題と呼ばれます。残念ながら、水素原子が水素分子になった瞬間、粒子数が多すぎてシュレディンガー方程式が解けなくなってしまうのです。そのため、いかにして系を近似するかというのが課題となっています。

摂動法

　偉い人は考えました。ハミルトニアンをちょっと動かせば固有関数もちょっと動くはずだと。つまり、元々のハミルトニアンと固有関数のセットを \hat{H_0}、 \varphi_0。ちょっと動かしたハミルトニアンを \hat{H}とすると、

\hat{H} =\hat{H_0} + \hat{H'}

 

この時、変化したエネルギーは、

 

E' = \int {\varphi_0}^* \hat{H'} \varphi_0 dr

 

と書くことができます。これを（一次の）摂動と呼びます。二次以降は今回扱いません。

ちなみに、波動関数は直行規格化しておかないと摂動の計算が大変なことになるので、規格直交基底で

ある前提でお話しします。

 

※規格直交規定とは：内積がクロネッカーのデルタになるような関数の集まりのこと。詳しくは調べてみてください。

 

変分法

　ってな訳で昔のえらい人(ヒュッケルさん)が、これをうまいこと処理できないかと考え、変分原理を用いた変分法を使ってみることにしました。変分原理とは、

\hat{H}\psi = E \psi

が成り立っている時、ハミルトニアンに固有関数でない、適当な偽の関数 \phi_aをかけると、


\hat{H}\phi_a = E' \phi_b

と計算ができてしまいます。この時現れた偽のエネルギーの値 E'と Eの間には、

E’\geqq E

という関係性があり、つまり、偽の関数でエネルギーを最小化できれば、正しい固有関数に近づくということです。この偽の関数のことを試験関数と呼び、この手法を変分法と呼びます。

 

ヒュッケル近似法

　それでは、ヒュッケルさんの本領発揮といたしましょう。ヒュッケル近似とは、炭素原子のπ電子からスタートして、非局在化による安定化エネルギーを摂動で取り扱います。

　試しにブタジエンで計算してみましょう。試験関数は左からn番目の炭素のπ電子を \varphi_nとして、

 

 \varPsi =  c_1\varphi_1 + c_2\varphi_2 + c_3\varphi_3 + c_4\varphi_4

 

各cはそのπ電子が分子の軌道にどのくらい寄与しているかの値です。

摂動エネルギーは、

 

E' = \int \varPsi^* \hat{H'} \varPsi dr

 

これを最小にするために、微分を使います。微分した値が0である点がエネルギー最小である（今回は簡単のため、極大や極小を考えません。）ということを使います。

両辺を c_1, c_2, c_3, c_4でそれぞれ微分する事で

 

c_1\alpha + c_2\beta =0

c_1\beta + c_2\alpha + c_3\beta = 0

c_2\beta + c_3\alpha + c_4\beta = 0

c_3\beta + c_4\alpha = 0

 

ただし、

\alpha = \int \varphi_n \hat{H'} \varphi_n

\beta = \int \varphi_n \hat{H'} \varphi_{n+1}

\beta = \int \varphi_{n-1} \hat{H'} \varphi_n

それ以外はゼロとしました。これをヒュッケル近似と呼びます。

\alphaのことを、自己積分と呼びます。よくよく見ると、自己積分はπ電子が持つ元々のエネルギーを表していることがわかります。

\betaのことを共鳴積分と呼び、隣接するπ電子の非局在化を表します。

 

とにかく、あの四元一次連立方程式さえ解くことが出来れば、エネルギーを求めることが出来そうです。

 

ところで、何かおかしなことに気が付きませんか？そう、みてわかる通り、 c_1=c_2=c_3=c_4=0が解になってしまうのです。それでは軌道が消えてしまい、何の意味も無くなってしまいます。これ以外の解を探すには、高校数学では残念ながら…

 

次回予告！

連立方程式解きます！代入したり消去したりだけが解法でないことを思い知らせてやる！

 

2020.06.06

【なんとなくわかる量子化学】第３回　解いてみようシュレディンガー方程式

なんとなくわかる量子化学 量子化学

シュレディンガー方程式を解く

　さてさてやっとこさ方程式を解くところまで来ましたね。でもシュレディンガー方程式は微分方程式だったので、高校数学で解くことができません。そこで、1次元井戸型ポテンシャルを例にして解き方を覚えてみましょう。

\displaystyle -\frac{\hbar^2}{2m_e}\frac{\partial^2 \psi }{\partial x^2} = E\psi

 

これが1次元のシュレディンガー方程式です。数学を使ってまともに解くこともできるのですが…我々化学の人間はちょっと難しいので、ズルいことをします。この方程式の形をよく見ると、二回微分しても元の関数の定数倍になっていると言うところから、 Ae^{ikx}という形を考えてみましょう

二回微分してみるとこんな感じ。


\displaystyle \frac{\partial^2}{\partial x^2} e^{ikx} =-k^2 e^{ikx}

 

シュレディンガー方程式を移項するとこんな感じ。

 

\displaystyle \frac{\partial^2}{\partial x^2} e^{ikx} = -\frac{2m_eE}{\hbar^2} e^{ikx}

 

見比べて、

 

\displaystyle k = \sqrt{\frac{2m_eE}{\hbar^2}}

 

を得ます。と言うわけで波動関数の完成だ！．…とは言ってもまだEの値がわからない。我々はエネルギーが知りたいのに…

 

井戸型ポテンシャルの境界条件

　実は、先程の方程式、普通に解くと E=0, \psi=0になってしまいます。これは大きなスケールで波動性が消えることにも関係しています。という訳でスケールを小さくするために、井戸型ポテンシャルと言うものを導入します。粒子を x=0と x=Lの間に閉じ込めてしまいましょう。すると、粒子の存在しないところに波動関数はないので、 \psi(0)=0と \psi(L)=0と言う条件が得られます。これを境界条件と呼びます。前回紹介したオイラーの式を使うと、

 

e^{ikx} = \cos kx + i\sin kx

 

であるので、波動関数として

 

\psi(x) = A\cos kx + Bi\sin kx

 

を採用することいたしましょう。しかし、 \psi(0) = Aなので、Aが0となり、コサインの項が消えます。さて、Bですが、波動関数の二乗が1となるように波動関数の係数を決めるというルール（規格化）があるので、結局、

 

\psi(x) = sinkx

 

が得られました。

f:id:sandcat_neco:20200515152000j:plain

井戸型ポテンシャルのイメージ図

エネルギーの量子化

　ところで、もうひとつの境界条件である \psi(L)=0を使っていませんね。これを波動関数に代入すると、

 

\sin kL = 0

 

が得られます。サインは多価関数なので、kLがπの倍数になるときに0の値をとります。故に、正の整数nに対し

 

\displaystyle k= \frac{n\pi}{L}

 

という関係式が成り立ち、両辺を二乗してkを代入してみると、

 

\displaystyle E_n = \frac{\pi^2 \hbar^2}{2m_eL^2} n^2 = \frac{h^2}{8m_eL^2}n^2

 

となります。ここで大事なのが、エネルギーが整数nの二乗で表されることです。n=1やn=2は大丈夫でもn=1.5といった条件は許されません。エネルギーが離散的な値になることを、量子化と言います。ミクロな世界では、エネルギーが量子化されてしまうということをよく覚えておきましょう。

 

応用例1 ベータカロテン

　とここまでなら物理学なのですが、化学の人間としては分子の性質を見てみたくなりませんか？いや、なる。ということでベータカロテンを1次元井戸型ポテンシャルだとみてエネルギーを計算してみましょう。 

f:id:sandcat_neco:20200515153929p:plain

ベータカロテン

　これがベータカロテンです。炭素22個からなる共役系を持ちます。ひとつの軌道に電子は2つ入ることができる（上向きスピンと下向きスピン）ので、n=11とn=12のエネルギー差を計算してみたいと思います。なお、電子は光のエネルギーを吸って、nが異なる軌道に移動することができます。これを電子の励起と呼びます。この時の光のエネルギーは、軌道のエネルギー差と同じでないといけないので、軌道のエネルギー差から吸収する光の波長、すなわちその分子の色を予測することができます。

f:id:sandcat_neco:20200515155103j:plain

ベータカロテンのエネルギーダイアグラム

　さて、一般的な二重結合の長さは134pmなので、21倍した2814pmをLに代入して、n=12と11のエネルギー差を計算すると、1135nmの光に相当することがわかります。実際の分子は500～600nm程度に吸収を持つので、倍程度の誤差がありますが、近似が荒いにも関わらずこの程度の誤差で済むこと自体、一次元井戸型ポテンシャルも捨てたものではありません。すごいよね！シュレディンガー方程式！

応用例2 ベンゼン

　共役系といえばこれ！のベンゼンについても計算してみたいと思います。ところが、1次元井戸型ポテンシャルと境界条件が異なり、リングを一周した時に元どおりにならない波は消えてしまうことを境界条件とします。つまり、リングの周をLとして、

 

\psi(x) = \psi(x+L)

 

が成り立ちます。これを解くには、 e^{ikx}型の関数を波動関数としておくと楽です。代入すると、

 

\psi(x) = e^{ikx}

\psi(x+L) = e^{ikx}e^{ikL}

 

が成り立ちます。よって、整数nに対して、

 

\displaystyle k = \frac{2n\pi}{L}

 

となり、

 

\displaystyle E = \frac{n^2 h^2}{2mL^2}

 

という結果が得られます。ここで重要なのが、nはゼロや負の整数を取ることができるといった点です。詳しくは説明しませんが、nと-nが区別できるうようになったと考えてください。一方で、両者のエネルギーは等しいので、エネルギーダイアグラムは以下のようになります。

f:id:sandcat_neco:20200515155057j:plain

ベンゼンのエネルギーダイアグラム

　よって、長さLを134pmの６倍である804pmとして、n=1からn=2への遷移エネルギーを計算すると、178.7nmの光に相当するエネルギーであることがわかります。実際、ベンゼンは200~300nmの光を吸うことが知られており、こちらも荒い近似なのにもかかわらずある程度正しい結果が得られて大満足です。むふん。

 

次回予告

シュレディンガー方程式が解けて僕、大満足！でもそうは問屋が卸さない！

そもそも、有機分子なのに原子核のことを考えていない時点でお察しだった！

原子核を考えて電子雲を考えるともう大変！次回！数学死す！勉強スタンバイ！

というわけで、次回は三体問題からスタートします。

 

 

 

 

【なんとなくわかる量子化学】第2回　電子の軌道を見てみよう

量子化学 なんとなくわかる量子化学

水素原子の波動関数

　それでは、前回の予告通り、水素原子の波動関数を見てみることとしましょう。通常、波動関数の（二乗）のことを「軌道」（二乗の時は電子雲）と呼びます。水素原子には、陽子と電子があるので、電子の運動エネルギーに陽子からのポテンシャルを考えなくてはいけませんので、ハミルトニアンはこうなります。Δのことをラプラシアンと呼び、下の式で表します。

 

\displaystyle \hat{H} = - \frac{\hbar ^2}{2m_e}\Delta_e-\frac{q_e ^2}{4 \pi \varepsilon_0 r}

 

\displaystyle \Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}

 

 

　最後の項はおなじみの静電ポテンシャルでございます。 一応解析的に解けるのですが、手計算では難しいので解を見てしまいましょう。

 

\varphi(r,\theta,\phi) =R(r)_{nl}  Y_{lm}(\theta,\phi)

 

な、なんじゃこりゃああああああ！！！！
r, \theta, \phiってなんだ？！？！ nってlってｍってなんだよ！！！！
ごもっともでございます。今回はこれがわかるようになっていきましょう。

 

動径関数と球面調和関数

　まず、 r, \theta, \phiの三つですが、これを「球面座標形式」といいます。理系の皆さんならよーく思い出していただけると高校で習っていたりするかもしれません。(私と世代が違うので内容が違うかも…)要するに、x,y,zの代わりに、原点からの距離 rとz軸からの角度 \theta、xy平面の偏角 \phiの三つで座標を表しているのです。水素は球体なので、この形式で解を表示したほうが簡単に書けるといった理由があるのです。
　それでは、RとYの説明に入っていきましょう。Rのことを、動径関数とよび、Yのことを球面調和関数と呼びます。wikipediaに詳しいことは書いてあるのですが、要するに常人にはとけません！一方で、動径関数と球面調和関数の掛け算で波動関数ができるので、動径関数と球面調和関数の一覧がすでに計算されています。そのうち一部を紹介しましょう。

 

動径関数

\displaystyle R_{10}(r) = 2a_0^{-\frac{3}{2}}e^{-\frac{r}{a_0}}

\displaystyle R_{20}(r) = \frac{1}{2\sqrt2}a_0^{-\frac{3}{2}} \left (2-\frac{r}{a_0}\right) e^{-\frac{r}{2a_0}}

\displaystyle R_{21}(r) = \frac{1}{2\sqrt6}a_0^{-\frac{3}{2}}\left(\frac{r}{a_0} \right) e^{-\frac{r}{2a_0}}

 

球面調和関数

\displaystyle Y_{00}(\theta, \phi) = \frac{1}{2\sqrt{\pi}}

\displaystyle Y_{10}(\theta, \phi) = \frac{1}{2} \sqrt{\frac{3}{\pi}} \cos \theta

\displaystyle Y_{11} (\theta, \phi)= \frac{1}{2} \sqrt{\frac{3}{\pi}} \sin \theta e^{i\phi}

\displaystyle Y_{1-1}(\theta, \phi) = \frac{1}{2} \sqrt{\frac{3}{\pi}} \sin \theta e^{-i\phi}

 

なんかよくわからんけどそういうものです。気合がある人は自分で導出してみてください。

 

波動関数を作ろう！

　というわけでやっとこさ波動関数を作ることができるようになりました。波動関数 \PsiとRやYとの関係式は、以下のようになっています。

 

\displaystyle \Psi_{nlm} = R_{nl}Y_{lm}

 

波動関数はnlmの三つの整数で表すことができます。これを量子数といいます。nを主量子数、lを方位量子数、mを磁気量子数といいます。名前はテストに出やすいので覚えておきましょうね。また、

n-1\geqq l\geqq0

l \geqq m \geqq -l\

という制約があります。n=2ならば、lは0か1しか取れません。l=1ならmは-1,0,1の三種類ということになりますね。

先ほどのRの二つの数字がnlで、Yはlmの量子数を持っているので、lが同じ組み合わせでないとRとYを組み合わせることができません。具体的には…

 

\displaystyle \Psi_{100} = R_{10}Y_{00} = \frac{1}{\sqrt{\pi}}a_0^{-\frac{3}{2}}e^{-\frac{r}{a_0}}

\displaystyle \Psi_{210} = R_{21}Y_{10} = \frac{1}{4}\sqrt{\frac{3}{2\pi}}a_0^{-\frac{3}{2}} \left (2-\frac{r}{a_0}\right) e^{-\frac{r}{2a_0}}  \cos \theta

 

f:id:sandcat_neco:20200513132252p:plain
f:id:sandcat_neco:20200513132353p:plain
炭素ψ(100)（左）と炭素ψ(210)（右）

この結果をプロットするとこんな感じです。左のような球形の軌道のことをs軌道、右のようなダンベル型の軌道のことをp軌道といいます。d軌道やf軌道なんてのもあります。もしよかったら調べてみてください。

基底の取り直し

ところで、 Y_{11}と Y_{1-1}が複素数であることにお気づきでしょうか。複素数の座標ってなんだ…？というわけでどうにかして実数にしたい訳です。というわけでオイラーの公式を使ってみましょう。

 

\displaystyle e^{i\phi} = \cos\theta + i\sin\theta

\displaystyle e^{-i\phi} = \cos\theta - i\sin\theta

 

これより、

\displaystyle e^{i\phi} + e^{-i\phi} =  2\cos\theta

\displaystyle -ie^{i\phi} + ie^{-i\phi} =  2\sin\theta

 

これを利用すると、 Y_{11}と Y_{1-1}から、

\displaystyle Y_{px} = \frac{1}{2}\sqrt{\frac{3}{\pi}}\sin\theta\cos\phi

\displaystyle Y_{py} = \frac{1}{2}\sqrt{\frac{3}{\pi}}\sin\theta\sin\phi

となり、見事実数になります。

詳しい話をすると、これらの波動関数は同じ固有エネルギーを持つ（縮重という）ため、これらの波動関数を定数倍して足してもまた波動関数になるという特徴を持ちます。これは線形代数学からわかります。

今出てきた p_xや p_yに加えて、 p_z=\Psi_{210}の三種類のp軌道を導くことができました。

 

エネルギーを見てみよう！

　さて、やっとこさエネルギーの話になってきました。先ほど得られた波動関数をハミルトニアンにかけてみると、結果は

\displaystyle E = -\frac{me^4}{8\varepsilon_0^2 h^2}\frac{1}{n^2}

ぬぁんと！主量子数にしか影響しないのです！おっぱげた！

しかもnの逆二乗ってなにか見覚えありませんか…そう、リュードベリのアレです！というわけで、 E=h\frac{c}{\lambda}を代入すると、

 

\displaystyle \frac{1}{\lambda} =\frac{me^4}{8\varepsilon_0^2 h^3 c}\frac{1}{n^2} =R_H\frac{1}{n^2}

 

ってな感じでリュードベリ定数が出てきてしまいました。難しかったけど、どうやら答えはあっているようで安心しましたね。めでたしめでた…ちょっと待った！分子になったら一体全体軌道はどうなってしまうんだ？！

 

次回予告

分子の軌道をモデルで近似して解いてみよう！　こうご期待！

f:id:sandcat_neco:20200513163725p:plain

ベンゼンの分子軌道

 

やってみよう量子化学計算! WinmostarでやるMOPAC入門

量子化学

はじめに

いぇーいみんな量子化学計算してるー？してない？してるわけねーだろって？そうだよね。つよいサーバーとgaussianのライセンスいるもんね…

　でも精度は低いものの、ノートPCレベルのスペックで量子化学計算ができるフリーソフトがあるのです。その名もWinmostar! このパッケージにはMOPAC6というソフトが含まれており、ボタン一つでぽちっと計算できちゃうのです。というわけでお前も量子化学計算やるんだよ！！！！

ソフトウェアの導入

Winmostar

https://winmostar.com/jp/dlFreeForm.php

このリンクに自分のメールアドレスを入力するとDLアドレスとライセンスが送られてきます。もし大学のアドレスを持っているなら、学生版にチェックして大学のアドレスを入力することで、ちょっとだけいい機能のものを使うことができますよ。MOPACは無償版でも使えます。

 

Chemsketch

https://www.acdlabs.com/resources/freeware/chemsketch/download.php

これは構造式を描画するソフトウェアです。こちらで構造を作っておいて、Winmostarで読み込むとはかどります。もしChemdrawや別のソフトウェアが持っている場合はそちらでもokです。

 

さっそくやってみよう！

1.構造式を作ろう！

まずは元となる構造式をChemsketchで書きます。

f:id:sandcat_neco:20200418002457p:plain

きたないポルフィリン

汚ったねぇなぁ！でも大丈夫！このボタンならね

f:id:sandcat_neco:20200418002738p:plain

魔法のボタン(Clean structure)

右上の方にあるこのボタンをぽちっと押すと、

f:id:sandcat_neco:20200418002821p:plain

きれいなポルフィリン

綺麗なポルフィリンになりました。これをFileから名前を付けて保存で、.mol形式にしてしまいましょう。

左上のFile→Saveas→ドロップダウンで.molを選択して保存します。

f:id:sandcat_neco:20200418003111p:plain

.molの選び方

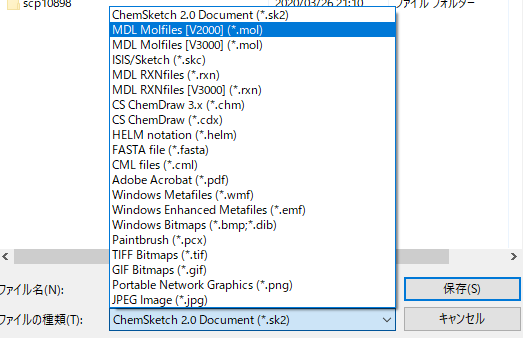
2.Winmostarで構造を整えよう！

早速Winmostarを起動して、先ほどのmolファイルをドラッグアンドドロップしてみましょう。

f:id:sandcat_neco:20200418003333p:plain

Winmostarにmolファイルを読み込ませたところ

おや…？水素原子がありませんね。実は先ほどのmolファイルには水素原子が含まれていませんでした。水素原子を付けるには、chemsketch上でTool→Add Explicit Hydrogenを選ぶまたは、

f:id:sandcat_neco:20200418003639p:plain

Chemsketch上で水素原子を足す方法

Winmostar上で編集→水素を付加→すべての原子に付加をしましょう。

f:id:sandcat_neco:20200418003859p:plain

Winmostar上で水素を足す方法

水素がついたら、右上にあるほうきマークをクリックして、構造をきれいにします。

f:id:sandcat_neco:20200418004045p:plain

ほうきマーク

これをやっておくと計算の収束が早くなります。

3.計算しよう！

では早速計算してみましょう。

f:id:sandcat_neco:20200418004646p:plain

MOPAC実行

MOP6W70実行を選択して、適当な名前で保存しちゃいましょう。何やら黒い画面に大量の文字が流れていきます。

f:id:sandcat_neco:20200418005034p:plain

大量の文字

　CYCLEは計算の回数、TIMEは1回にかかった時間、LEFTは計算の残り時間(3600秒以上かかる場合は計算ができなかったものとして勝手に終わります。)、GRADはエネルギー勾配で、この値が小さいほど収束が近いです。最後にHEATは生成熱です。これが最小値になるように計算していきます。

　上の方のCYCLE12ではGRADが4桁なのに対し、CYCLE40では0.144と相当小さくなっていますね。HEATも478から242まで下がっています。GRADがある値以下になったとき、構造最適化が終わったと判断して計算が終わります。

4.エネルギーと分子軌道を見てみよう！

f:id:sandcat_neco:20200418005624p:plain

エネルギーと分子軌道を見てみよう

計算が終わったら、この図のように分子軌道、電子密度(mgf)を選び、(名前).mgfを開きましょう。

f:id:sandcat_neco:20200418005811p:plain

.mgfを選ぶ

　今回はpolという名前を付けたので、pol.mgfを選びます。

f:id:sandcat_neco:20200418010016p:plain

mgfファイルを開いた結果

　左側がエネルギーダイアグラムです。わかりやすいようにeVにチェックしてあります。a.u.はeVの27.2114分の1の値です。量子化学計算では都合のいい値なので、a.u.で結果が出ることがあります。その場合は27.2114倍してくださいね。

　さて、左上にHOMO:57と出ていますので、57番の軌道がHOMOであることが分かります。ということは58番がLUMOですね。WinmostarはやさしいのでHOMO-LUMOギャップまで計算してくれています。

　早速HOMOを見てみましょう。Selected MOを57番にして、いざDraw!

f:id:sandcat_neco:20200418010519p:plain

ポルフィリンのHOMO(isoval=0.03)

　こんな結果になりました。なんかその…よくわからないですね…。このDrawでは、電子密度が一定のラインを表示してくれるモードなので、電子密度がちょうど0.03の境界線を表示しています。これだと軌道が小さすぎて、よく見えないので、Isosurface Valueを0.01にしてみましょう。

 

f:id:sandcat_neco:20200418010710p:plain

ポルフィリンのHOMO(isoval=0.01)

　分子全体に共役系が伸びている様子がよくわかりますね！また、表示をmeshからsmoothに変えることで、

f:id:sandcat_neco:20200418011133p:plain

ポルフィリンのHOMO(isoval=0.01, smooth)

　きれいな図になりました！せっかくなのでLUMOも見てみましょう。LUMOは58番だったので、Selected MOを58にしていざDraw!

f:id:sandcat_neco:20200418011320p:plain

Selected MOを58番にします。

f:id:sandcat_neco:20200418011355p:plain

ポルフィリンのLUMO(isoval=0.01, smooth)

　LUMOも無事描くことに成功しました！やったね！ちなみにHOMOとLUMOをよく見比べると、節の数がLUMOの方が多いことに気が付きます。

f:id:sandcat_neco:20200418011753p:plain

HOMO(左)とLUMO(右)

　そのうち量子化学の記事でも触れますが、節(赤と青の境界線のことです)が、HOMOは8か所、LUMOは10か所存在します。一般に節の数が多ければ高いエネルギーを持つということが知られており、ポルフィリンでも確かに成り立っていることが分かりますね。(σh面も節だけどわかる人はわかるよね…)

おわり。

　さて手ほどきは済んだのでみんな好きな分子を計算にかけてみよう！なお、このMOPACは半経験的な方法で、Gaussianがとっている非経験的(Ab initio)ではありませんので、変な分子には変な結果を返すことがあります。ご了承くださいまし。

　また、精度もそーんなには良くなく、GaussianでB3LYP/3-21Gで計算した結果と比べるとこんな感じです。(マシンスペックの関係で3-21Gですが、論文に出すなら最低でもB3LYP/6-31G*で計算してください。)

f:id:sandcat_neco:20200418020808p:plain

gaussianで計算したHOMO

f:id:sandcat_neco:20200418020845p:plain

gaussianで計算したLUMO

 MOPACの結果と軌道の形がちょこっとだけ違いますね。エネルギーも

 

  MOPAC Gaussian
HOMO -7.793 -5.335
LUMO -1.409 -2.237

 

 1eV程度のスケールで違いますね。1eVは化学の世界ではとても大きな違いです。なので、エネルギーを考えるときは参考程度に…。もちろん、Gaussianでもあっている保証はないですけどね。

ちょっと難しい話

　現実の系では、溶媒や他の分子との相互作用で軌道のエネルギーが変化することがあります。Gaussianでは溶媒もモデリングして計算することはできますが、これもまた発展途上です。例えば、溶媒を「分極が起きる場」と考えて近似する分極連続場モデル(https://ja.wikipedia.org/wiki/%E5%88%86%E6%A5%B5%E9%80%A3%E7%B6%9A%E4%BD%93%E3%83%A2%E3%83%87%E3%83%AB)もありますが、あくまで溶媒は形を持った分子なので、それ相応の結果しか与えてくれません。また、QM/MM法（https://ja.wikipedia.org/wiki/QM/MM）と呼ばれる、量子化学計算と分子動力学法(剛体近似みたいなものです。)を行い、タンパク質などの巨大分子を頑張って計算したりしていました。

　しかし、スーパーコンピューターの登場で、最近はCPUとメモリの暴力で大量の分子を第一原理的に計算をしようとする流れがあります。これにより、例えば固体表面での分子の挙動を計算することで固体触媒の反応機構を理解できたり、溶液中の分子の水素結合の挙動を見ることができるようになったりして、今まで手が付けられなかった分野にも計算化学が手を出せるようになるはずです。

　最近、スーパーコンピューター京の後継機として、富岳が開発され、運用が始まっています。（https://japanese.engadget.com/2019/12/03/supercomputer/）富岳三十六景にあやかった名前も粋ですが、富岳がどんな成果を出してくれるかも楽しみですね。

 

2020.4.18

【なんとなくわかる量子化学】第一回　シュレディンガー方程式ってなんなんだ？

量子化学 なんとなくわかる量子化学

はじめに

　この連載記事は、化学系学部一年生向けに、量子化学とはなんぞや？といった話をできるだけ易しく書いていきます。大学の授業ほど詳しくありませんが、化学を学ぶ人間にとって、シュレディンガー方程式がどのように使われて、何がうれしいのかを重点的に書いていく予定です。

 

　本記事は全5回程度の連載記事を予定しています。内容は、

 

・第一回　シュレディンガー方程式ってなんなんだ？

・第二回　電子の軌道をみてみよう

・第三回　解いてみようシュレディンガー方程式　

・第四回　やっぱり解けないシュレディンガー方程式を近似する

・第五回　意地でも解きたいので行列に頼ってみた

 

です。以上を話すうえで、第三回で微分方程式や第五回で行列の知識が必要になりますので、それも含まれています。特に、行列については今年度の学生は知らないと思いますので、かなり詳しく解説する予定です。

 

シュレディンガー方程式ってなんなんだ？

　まずはシュレディンガー方程式を見てみましょう。

\hat{H}\varphi=E\varphi 

訳が分かりませんね。でもこの方程式は、「ミクロな世界」の物事を表すことができるので、とても大切なのです。ミクロな世界では、我々の生きているマクロな世界と違う法則で動いていることが知られています。まずはこのルールについてみていきましょう。

ミクロな世界に潜むルール

　高校物理において、物質の運動はすべてニュートン式の古典力学で説明できるのでした。しかし、だんだんと研究が進むにつれて、古典力学で説明がつかないような現象が見つかってしまいました。

　代表的なものが、コンプトン効果です。波である光と物質である電子が相互作用するなんて当時の常識から外れていました。この結果から、「物質は波の性質も持つ」と無理やり言い張ったとんでもないおバカがいました。物質が波なんて訳が分かりません。そのせいで彼は学術界から孤立してしまったという話もあります。

　ですが、彼は正しかったのです。たしかに、「電子は物質でもあり波でもある」らしいのです。彼、すなわちドブロイは、ドブロイ波長といわれる波長を提案しました。

\displaystyle \lambda=\frac{h}{p}

λは波長、hはプランク定数、pは運動量を表します。プランク定数はなぜか量子の世界で出てくる定数です。(そういうことにしておいてください…込み入った話になるので…)つまり、運動量が大きいものは波長が小さいので、波としてふるまわないが、運動量が小さいものは波としてふるまうことができることを意味しています。

　このドブロイ波長をニュートン力学に組み込むことで生まれたのが先ほどのシュレディンガー方程式です。そして、φのことを波動関数、Hのことをハミルトニアンといいます。Eはエネルギーです。

 

ハミルトニアンと波動関数

  いきなりハミルトニアンだの、波動関数だのが出てきてしまいました。でも、これさえ分かれば、何とかシュレディンガー方程式が理解できそうです。

  まずは波動関数からいきましょう。波動関数は、言ってしまえばその状態の｢アカシックレコード｣です。上手く読み出せれば、その状態を何でもかんでも知ることができます。でもぶっちゃけそのままでは何も読めません。でも、演算子を使うと読み出すことができます。

  ハミルトニアンは、演算子と呼ばれるものの仲間です。演算子は、すぐ右の関数にイタズラをしてしまう困ったやつです。でも左側にはつーんとしていて何もしません。

 

\displaystyle \frac{\partial}{\partial x}

 

これは微分演算子と呼ばれるもので、すぐ右の関数を微分してしまいます。

 

\displaystyle \hat{p} = -i \hbar \frac{\partial}{\partial x}

 

これは運動量演算子と言って、微分演算子と定数値の組み合わせでできています。また、演算子が含まれる計算では、原則文字の入れ替えができないことを覚えておきましょう。

 

さて、ハミルトニアンの中身を具体的に見ていきましょう。自由電子のハミルトニアンは

 

\displaystyle \hat{H} = \frac{1}{2m_e}(\hat{p_x}^2 + \hat{p_y}^2 + \hat{p_z}^2)

 

運動量演算子の足し算と定数でハミルトニアンになっているようです。

…おや? 古典力学の世界では p=m_e vだったので、

 

\displaystyle \frac{1}{2m_e}(p_x ^2 + p_y ^2 + p_z ^2) = \frac{1}{2m_e}((m_e v_x )^2 + (m_e v_y) ^2+ (m_e v_x) ^2

\displaystyle = \frac{1}{2} m_e v ^2

 

なんとハミルトニアンは運動エネルギーに対応するのだ！

(正確にはその系に働く力を演算子にして、系のエネルギーの演算子にしたものをハミルトニアンと呼びます)

だから、ハミルトニアンを波動関数にぶつければ、エネルギーが分かる! なんともシンプルで素晴らしい方程式だ!

でもどうやって解くんだろう…さっぱりわからん。

とりあえず、具体的なハミルトニアンと波動関数を見てから考えることにしよう。というわけで次回は一番簡単な水素原子のシュレディンガー方程式の解を見ていきましょうね。

 

閑話休題 シュレディンガーの猫

 

  シュレディンガーの猫はご存知ですよね。猫は生きているか死んでいるか分からないというアレです。アレはよく間違った文脈で用いられるので、正しい歴史的経緯を話しましょう。

f:id:sandcat_neco:20200415025017p:plain

シュレディンガーの猫のイメージ図

from: https://commons.wikimedia.org/wiki/File:Schrodingers_cat.svg

  

シュレディンガー方程式は革新的なものでした。それこそアインシュタインがブーブー文句垂れるぐらいには大不評だったようです。その量子力学を批判する文脈で出てきた話がシュレディンガーの猫です。

  ラジウムとガイガーカウンター、毒薬と猫を用意し、ガイガーカウンターが反応したら毒薬の瓶を割るという装置を考えます。

  次回以降話すのですが、波動関数の絶対値を二乗してやることで粒子の存在確率を求めることができます。(ボルンの確率解釈)存在確率というものを正当化するために、｢様々な位置にいる電子の重ね合わせ｣という言い訳をしました。

   実際に装置を作動させてみましょう、ラジウムが放射線を出した状態と出していない状態は重ね合わせされています。これを無人で実験すると、毒薬の瓶が割れた状態と割れていない状態とで重ね合わせが起きているはずで、猫もまた生きている状態と死んでいる状態の重ね合わせが起きているはずです。

 

そんな訳あるかーーーーーー!!!!

 

といってシュレディンガー方程式は怒られたのでしたちゃんちゃん。

  でも確かに、ミクロで確率的に、マクロでは絶対的に振る舞うのは矛盾しているように見えます。言い換えれば、ミクロとマクロの境界線はどこだ?と問う問題でもあるのです。この話は現代においても議論を巻き起こす難しい問題です。

　一つ面白い話として、エーレンフェストの定理を紹介しておきます。詳しくはeman先生に話を譲るとして、(https://eman-physics.net/quantum/expectation.html)この定理は、シュレディンガー方程式に従う粒子は"マクロに"運動方程式にも従うということを言っています。つまるところ、シュレディンガー方程式と運動方程式は両立しうるものなのです。イメージとしては、「運動方程式を顕微鏡で覗いてみたらシュレディンガー方程式だった」という感じでしょうか。伝わるかな？

　とにかく、シュレディンガー方程式は突拍子もないようで、意外と古典物理と矛盾が無いことを言っているのです。不思議ですね。

　そんなこんなで第一回を終わりにしたいと思います。tex記法も勉強したしリモートワークで論文書くのもだるいし一杯ブログ書くぞえいえいおー(はよ論文書け)

 

 2020.04.15